PINE LIBRARY
FunctionBaumWelch
Cập nhật
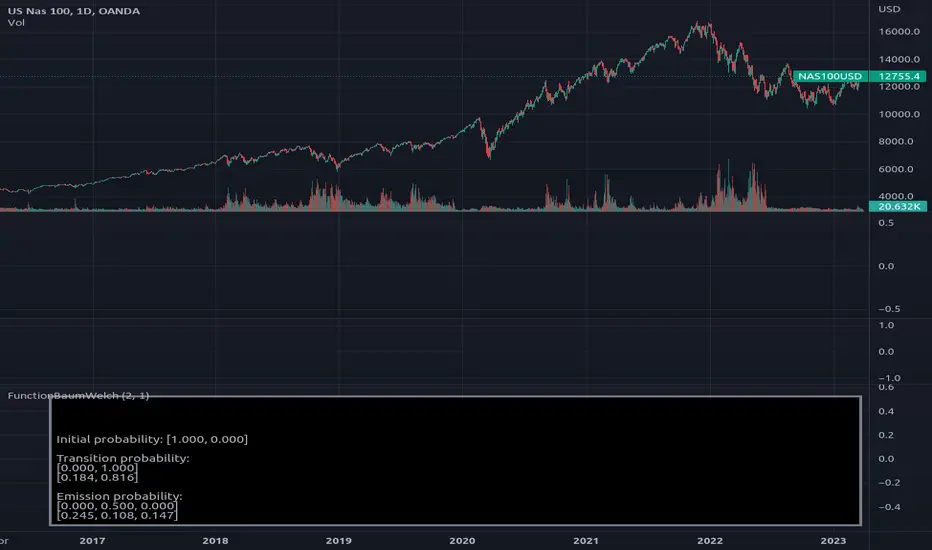
Library "FunctionBaumWelch"
Baum-Welch Algorithm, also known as Forward-Backward Algorithm, uses the well known EM algorithm
to find the maximum likelihood estimate of the parameters of a hidden Markov model given a set of observed
feature vectors.
---
### Function List:
> `forward (array<float> pi, matrix<float> a, matrix<float> b, array<int> obs)`
> `forward (array<float> pi, matrix<float> a, matrix<float> b, array<int> obs, bool scaling)`
> `backward (matrix<float> a, matrix<float> b, array<int> obs)`
> `backward (matrix<float> a, matrix<float> b, array<int> obs, array<float> c)`
> `baumwelch (array<int> observations, int nstates)`
> `baumwelch (array<int> observations, array<float> pi, matrix<float> a, matrix<float> b)`
---
### Reference:
> en.wikipedia.org/wiki/Baum–Welch_algorithm
> github.com/alexsosn/MarslandMLAlgo/blob/4277b24db88c4cb70d6b249921c5d21bc8f86eb4/Ch16/HMM.py
> en.wikipedia.org/wiki/Forward_algorithm
> rdocumentation.org/packages/HMM/versions/1.0.1/topics/forward
> rdocumentation.org/packages/HMM/versions/1.0.1/topics/backward
forward(pi, a, b, obs)
Computes forward probabilities for state `X` up to observation at time `k`, is defined as the
probability of observing sequence of observations `e_1 ... e_k` and that the state at time `k` is `X`.
Parameters:
pi (float[]): Initial probabilities.
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing
states given a state matrix is size (M x M) where M is number of states.
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. Given
state matrix is size (M x O) where M is number of states and O is number of different
possible observations.
obs (int[]): List with actual state observation data.
Returns: - `matrix<float> _alpha`: Forward probabilities. The probabilities are given on a logarithmic scale (natural logarithm). The first
dimension refers to the state and the second dimension to time.
forward(pi, a, b, obs, scaling)
Computes forward probabilities for state `X` up to observation at time `k`, is defined as the
probability of observing sequence of observations `e_1 ... e_k` and that the state at time `k` is `X`.
Parameters:
pi (float[]): Initial probabilities.
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing
states given a state matrix is size (M x M) where M is number of states.
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. Given
state matrix is size (M x O) where M is number of states and O is number of different
possible observations.
obs (int[]): List with actual state observation data.
scaling (bool): Normalize `alpha` scale.
Returns: - #### Tuple with:
> - `matrix<float> _alpha`: Forward probabilities. The probabilities are given on a logarithmic scale (natural logarithm). The first
dimension refers to the state and the second dimension to time.
> - `array<float> _c`: Array with normalization scale.
backward(a, b, obs)
Computes backward probabilities for state `X` and observation at time `k`, is defined as the probability of observing the sequence of observations `e_k+1, ... , e_n` under the condition that the state at time `k` is `X`.
Parameters:
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing states
given a state matrix is size (M x M) where M is number of states
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. given state
matrix is size (M x O) where M is number of states and O is number of different possible observations
obs (int[]): Array with actual state observation data.
Returns: - `matrix<float> _beta`: Backward probabilities. The probabilities are given on a logarithmic scale (natural logarithm). The first dimension refers to the state and the second dimension to time.
backward(a, b, obs, c)
Computes backward probabilities for state `X` and observation at time `k`, is defined as the probability of observing the sequence of observations `e_k+1, ... , e_n` under the condition that the state at time `k` is `X`.
Parameters:
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing states
given a state matrix is size (M x M) where M is number of states
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. given state
matrix is size (M x O) where M is number of states and O is number of different possible observations
obs (int[]): Array with actual state observation data.
c (float[]): Array with Normalization scaling coefficients.
Returns: - `matrix<float> _beta`: Backward probabilities. The probabilities are given on a logarithmic scale (natural logarithm). The first dimension refers to the state and the second dimension to time.
baumwelch(observations, nstates)
**(Random Initialization)** Baum–Welch algorithm is a special case of the expectation–maximization algorithm used to find the
unknown parameters of a hidden Markov model (HMM). It makes use of the forward-backward algorithm
to compute the statistics for the expectation step.
Parameters:
observations (int[]): List of observed states.
nstates (int)
Returns: - #### Tuple with:
> - `array<float> _pi`: Initial probability distribution.
> - `matrix<float> _a`: Transition probability matrix.
> - `matrix<float> _b`: Emission probability matrix.
---
requires: `import RicardoSantos/WIPTensor/2 as Tensor`
baumwelch(observations, pi, a, b)
Baum–Welch algorithm is a special case of the expectation–maximization algorithm used to find the
unknown parameters of a hidden Markov model (HMM). It makes use of the forward-backward algorithm
to compute the statistics for the expectation step.
Parameters:
observations (int[]): List of observed states.
pi (float[]): Initial probaility distribution.
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing states
given a state matrix is size (M x M) where M is number of states
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. given state
matrix is size (M x O) where M is number of states and O is number of different possible observations
Returns: - #### Tuple with:
> - `array<float> _pi`: Initial probability distribution.
> - `matrix<float> _a`: Transition probability matrix.
> - `matrix<float> _b`: Emission probability matrix.
---
requires: `import RicardoSantos/WIPTensor/2 as Tensor`
Baum-Welch Algorithm, also known as Forward-Backward Algorithm, uses the well known EM algorithm
to find the maximum likelihood estimate of the parameters of a hidden Markov model given a set of observed
feature vectors.
---
### Function List:
> `forward (array<float> pi, matrix<float> a, matrix<float> b, array<int> obs)`
> `forward (array<float> pi, matrix<float> a, matrix<float> b, array<int> obs, bool scaling)`
> `backward (matrix<float> a, matrix<float> b, array<int> obs)`
> `backward (matrix<float> a, matrix<float> b, array<int> obs, array<float> c)`
> `baumwelch (array<int> observations, int nstates)`
> `baumwelch (array<int> observations, array<float> pi, matrix<float> a, matrix<float> b)`
---
### Reference:
> en.wikipedia.org/wiki/Baum–Welch_algorithm
> github.com/alexsosn/MarslandMLAlgo/blob/4277b24db88c4cb70d6b249921c5d21bc8f86eb4/Ch16/HMM.py
> en.wikipedia.org/wiki/Forward_algorithm
> rdocumentation.org/packages/HMM/versions/1.0.1/topics/forward
> rdocumentation.org/packages/HMM/versions/1.0.1/topics/backward
forward(pi, a, b, obs)
Computes forward probabilities for state `X` up to observation at time `k`, is defined as the
probability of observing sequence of observations `e_1 ... e_k` and that the state at time `k` is `X`.
Parameters:
pi (float[]): Initial probabilities.
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing
states given a state matrix is size (M x M) where M is number of states.
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. Given
state matrix is size (M x O) where M is number of states and O is number of different
possible observations.
obs (int[]): List with actual state observation data.
Returns: - `matrix<float> _alpha`: Forward probabilities. The probabilities are given on a logarithmic scale (natural logarithm). The first
dimension refers to the state and the second dimension to time.
forward(pi, a, b, obs, scaling)
Computes forward probabilities for state `X` up to observation at time `k`, is defined as the
probability of observing sequence of observations `e_1 ... e_k` and that the state at time `k` is `X`.
Parameters:
pi (float[]): Initial probabilities.
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing
states given a state matrix is size (M x M) where M is number of states.
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. Given
state matrix is size (M x O) where M is number of states and O is number of different
possible observations.
obs (int[]): List with actual state observation data.
scaling (bool): Normalize `alpha` scale.
Returns: - #### Tuple with:
> - `matrix<float> _alpha`: Forward probabilities. The probabilities are given on a logarithmic scale (natural logarithm). The first
dimension refers to the state and the second dimension to time.
> - `array<float> _c`: Array with normalization scale.
backward(a, b, obs)
Computes backward probabilities for state `X` and observation at time `k`, is defined as the probability of observing the sequence of observations `e_k+1, ... , e_n` under the condition that the state at time `k` is `X`.
Parameters:
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing states
given a state matrix is size (M x M) where M is number of states
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. given state
matrix is size (M x O) where M is number of states and O is number of different possible observations
obs (int[]): Array with actual state observation data.
Returns: - `matrix<float> _beta`: Backward probabilities. The probabilities are given on a logarithmic scale (natural logarithm). The first dimension refers to the state and the second dimension to time.
backward(a, b, obs, c)
Computes backward probabilities for state `X` and observation at time `k`, is defined as the probability of observing the sequence of observations `e_k+1, ... , e_n` under the condition that the state at time `k` is `X`.
Parameters:
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing states
given a state matrix is size (M x M) where M is number of states
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. given state
matrix is size (M x O) where M is number of states and O is number of different possible observations
obs (int[]): Array with actual state observation data.
c (float[]): Array with Normalization scaling coefficients.
Returns: - `matrix<float> _beta`: Backward probabilities. The probabilities are given on a logarithmic scale (natural logarithm). The first dimension refers to the state and the second dimension to time.
baumwelch(observations, nstates)
**(Random Initialization)** Baum–Welch algorithm is a special case of the expectation–maximization algorithm used to find the
unknown parameters of a hidden Markov model (HMM). It makes use of the forward-backward algorithm
to compute the statistics for the expectation step.
Parameters:
observations (int[]): List of observed states.
nstates (int)
Returns: - #### Tuple with:
> - `array<float> _pi`: Initial probability distribution.
> - `matrix<float> _a`: Transition probability matrix.
> - `matrix<float> _b`: Emission probability matrix.
---
requires: `import RicardoSantos/WIPTensor/2 as Tensor`
baumwelch(observations, pi, a, b)
Baum–Welch algorithm is a special case of the expectation–maximization algorithm used to find the
unknown parameters of a hidden Markov model (HMM). It makes use of the forward-backward algorithm
to compute the statistics for the expectation step.
Parameters:
observations (int[]): List of observed states.
pi (float[]): Initial probaility distribution.
a (matrix<float>): Transmissions, hidden transition matrix a or alpha = transition probability matrix of changing states
given a state matrix is size (M x M) where M is number of states
b (matrix<float>): Emissions, matrix of observation probabilities b or beta = observation probabilities. given state
matrix is size (M x O) where M is number of states and O is number of different possible observations
Returns: - #### Tuple with:
> - `array<float> _pi`: Initial probability distribution.
> - `matrix<float> _a`: Transition probability matrix.
> - `matrix<float> _b`: Emission probability matrix.
---
requires: `import RicardoSantos/WIPTensor/2 as Tensor`
Phát hành các Ghi chú
v2 minor update.Phát hành các Ghi chú
Fix logger version.Phát hành các Ghi chú
v4 - Added error checking for some errors.Phát hành các Ghi chú
v5 - Improved calculation by merging some of the loops, where possible.Thư viện Pine
Theo tinh thần TradingView thực sự, tác giả đã xuất bản mã Pine này dưới dạng thư viện nguồn mở để các lập trình viên Pine khác trong cộng đồng của chúng tôi có thể sử dụng lại. Chúc mừng tác giả! Bạn có thể sử dụng thư viện này riêng tư hoặc trong các bài đăng nguồn mở khác. Tuy nhiên, bạn cần sử dụng lại mã này theo Quy tắc nội bộ.
Thông báo miễn trừ trách nhiệm
Thông tin và ấn phẩm không có nghĩa là và không cấu thành, tài chính, đầu tư, kinh doanh, hoặc các loại lời khuyên hoặc khuyến nghị khác được cung cấp hoặc xác nhận bởi TradingView. Đọc thêm trong Điều khoản sử dụng.