Smoothed Delta's Ratio Oscillator
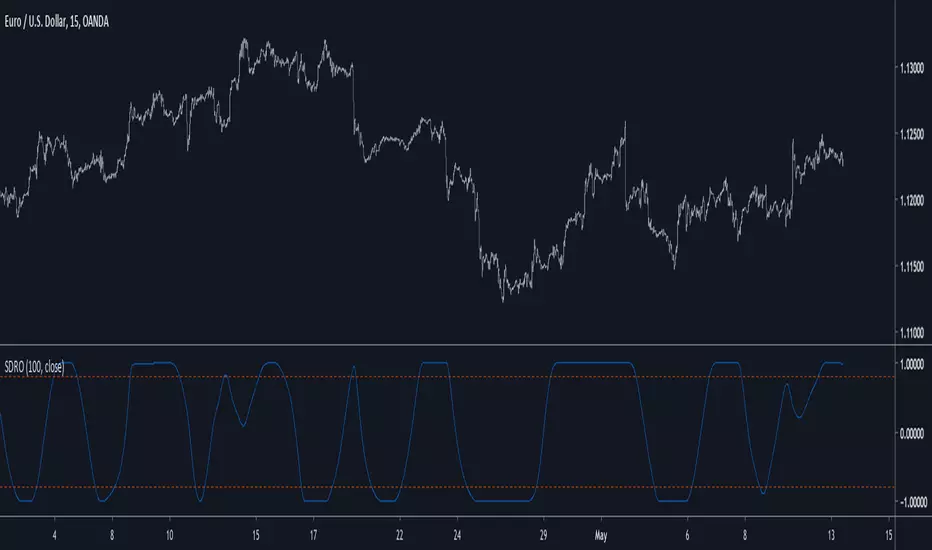
Introduction
Scaled and smoothed oscillators can provide easy to read/use information regarding price, therefore i will introduce a new oscillator who create smooth results and use a fast and practical scaling method. In order to allow for even more smoothness the option to smooth the input with a lsma has been added.
Scaling Using Changes
In this indicator scaling in a range of (1,-1) is achieved through the following calculations :
where src is our input. The two elements a and b are quite similar, a smooth the absolute change of the input over length period while b calculate the change of the smoothed input over length period, this make a > b and able us to perform scaling in a range of (1,-1).
The Indicator Parameters
Length control the differencing/smoothing period of the indicator, greater values create smoother and less volatile results, this mean that the oscillator will tend to be equal to 1 or -1 in a longer period of time if length is high. The smooth option allow for even smoother results by enabling the input to be smoothed by a lsma of length period.
Conclusions
I presented a smooth oscillator using a new rescaling technique. Parameters can be separated to provide different results, i believe the code is simple enough for everyone to modify it in order to provide interesting creations.
Scaled and smoothed oscillators can provide easy to read/use information regarding price, therefore i will introduce a new oscillator who create smooth results and use a fast and practical scaling method. In order to allow for even more smoothness the option to smooth the input with a lsma has been added.
Scaling Using Changes
In this indicator scaling in a range of (1,-1) is achieved through the following calculations :
- a = sma(abs(change(src,length)),length)
- b = change(sma(src,length),length)
- c = b/a
where src is our input. The two elements a and b are quite similar, a smooth the absolute change of the input over length period while b calculate the change of the smoothed input over length period, this make a > b and able us to perform scaling in a range of (1,-1).
The Indicator Parameters
Length control the differencing/smoothing period of the indicator, greater values create smoother and less volatile results, this mean that the oscillator will tend to be equal to 1 or -1 in a longer period of time if length is high. The smooth option allow for even smoother results by enabling the input to be smoothed by a lsma of length period.
Conclusions
I presented a smooth oscillator using a new rescaling technique. Parameters can be separated to provide different results, i believe the code is simple enough for everyone to modify it in order to provide interesting creations.
Check out the indicators we are making at luxalgo: www.tradingview.com/u/LuxAlgo/