PINE LIBRARY
Cập nhật FunctionBlackScholes
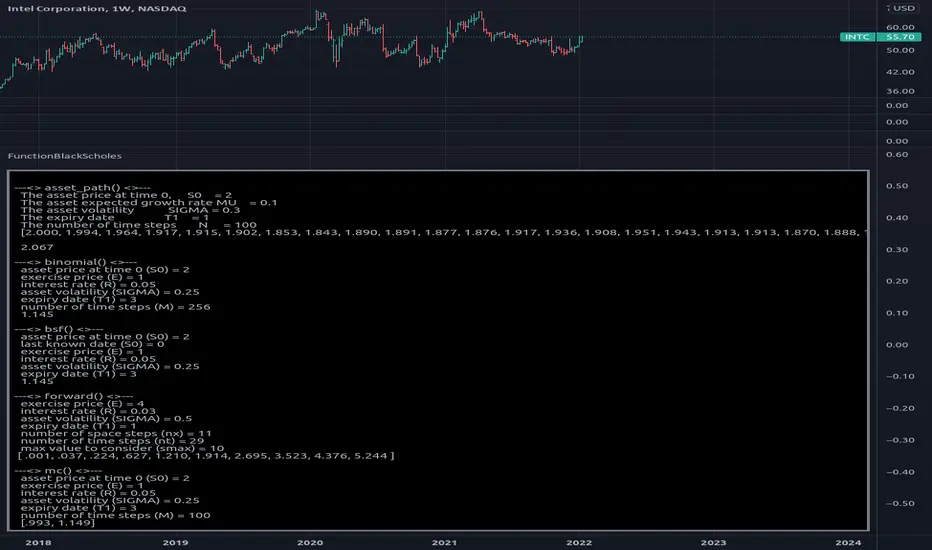
Library "FunctionBlackScholes"
Some methods for the Black Scholes Options Model, which demonstrates several approaches to the valuation of a European call.
// reference:
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.html
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.py
asset_path(s0, mu, sigma, t1, n) Simulates the behavior of an asset price over time.
Parameters:
s0: float, asset price at time 0.
mu: float, growth rate.
sigma: float, volatility.
t1: float, time to expiry date.
n: int, time steps to expiry date.
Returns: option values at each equal timed step (0 -> t1)
binomial(s0, e, r, sigma, t1, m) Uses the binomial method for a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: option value at time 0.
bsf(s0, t0, e, r, sigma, t1) Evaluates the Black-Scholes formula for a European call.
Parameters:
s0: float, asset price at time 0.
t0: float, time at which the price is known.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
Returns: option value at time 0.
forward(e, r, sigma, t1, nx, nt, smax) Forward difference method to value a European call option.
Parameters:
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
nx: int, number of space steps in interval (0, L).
nt: int, number of time steps.
smax: float, maximum value of S to consider.
Returns: option values for the european call, float array of size ((nx-1) * (nt+1)).
mc(s0, e, r, sigma, t1, m) Uses Monte Carlo valuation on a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: confidence interval for the estimated range of valuation.
Some methods for the Black Scholes Options Model, which demonstrates several approaches to the valuation of a European call.
// reference:
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.html
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.py
asset_path(s0, mu, sigma, t1, n) Simulates the behavior of an asset price over time.
Parameters:
s0: float, asset price at time 0.
mu: float, growth rate.
sigma: float, volatility.
t1: float, time to expiry date.
n: int, time steps to expiry date.
Returns: option values at each equal timed step (0 -> t1)
binomial(s0, e, r, sigma, t1, m) Uses the binomial method for a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: option value at time 0.
bsf(s0, t0, e, r, sigma, t1) Evaluates the Black-Scholes formula for a European call.
Parameters:
s0: float, asset price at time 0.
t0: float, time at which the price is known.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
Returns: option value at time 0.
forward(e, r, sigma, t1, nx, nt, smax) Forward difference method to value a European call option.
Parameters:
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
nx: int, number of space steps in interval (0, L).
nt: int, number of time steps.
smax: float, maximum value of S to consider.
Returns: option values for the european call, float array of size ((nx-1) * (nt+1)).
mc(s0, e, r, sigma, t1, m) Uses Monte Carlo valuation on a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: confidence interval for the estimated range of valuation.
Phát hành các Ghi chú
v2 fixed some issues.Thư viện Pine
Theo đúng tinh thần TradingView, tác giả đã công bố mã Pine này như một thư viện mã nguồn mở để các lập trình viên Pine khác trong cộng đồng có thể tái sử dụng. Chúc mừng tác giả! Bạn có thể sử dụng thư viện này cho mục đích cá nhân hoặc trong các ấn phẩm mã nguồn mở khác, nhưng việc tái sử dụng mã này trong các ấn phẩm phải tuân theo Nội Quy.
Thông báo miễn trừ trách nhiệm
Thông tin và các ấn phẩm này không nhằm mục đích, và không cấu thành, lời khuyên hoặc khuyến nghị về tài chính, đầu tư, giao dịch hay các loại khác do TradingView cung cấp hoặc xác nhận. Đọc thêm tại Điều khoản Sử dụng.
Thư viện Pine
Theo đúng tinh thần TradingView, tác giả đã công bố mã Pine này như một thư viện mã nguồn mở để các lập trình viên Pine khác trong cộng đồng có thể tái sử dụng. Chúc mừng tác giả! Bạn có thể sử dụng thư viện này cho mục đích cá nhân hoặc trong các ấn phẩm mã nguồn mở khác, nhưng việc tái sử dụng mã này trong các ấn phẩm phải tuân theo Nội Quy.
Thông báo miễn trừ trách nhiệm
Thông tin và các ấn phẩm này không nhằm mục đích, và không cấu thành, lời khuyên hoặc khuyến nghị về tài chính, đầu tư, giao dịch hay các loại khác do TradingView cung cấp hoặc xác nhận. Đọc thêm tại Điều khoản Sử dụng.