TASC 2023.05 Cong Adaptive Moving Average

14 thg 4, 2023

█ OVERVIEW

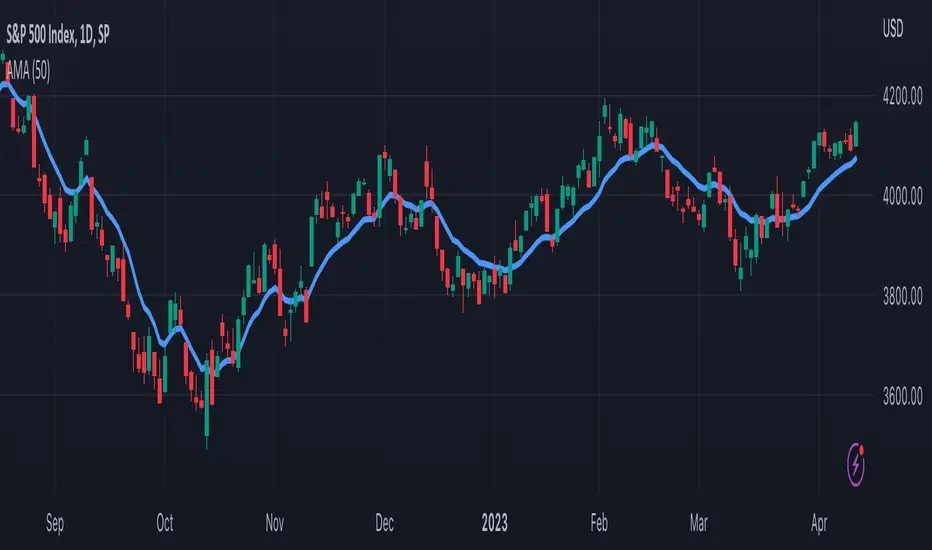
TASC's May 2023 edition of Traders' Tips features an article titled "An Adaptive Moving Average For Swing Trading" by Scott Cong. The article presents a new adaptive moving average (​AMA) that adjusts its parameters automatically based on market volatility. The ​AMA tracks price closely during trending movements and remains flat during congestion areas.

█ CONCEPTS

Conventional moving averages (MAs) use a fixed lookback period, which may lead to limited performance in constantly changing market conditions. Perry ​Kaufman's adaptive moving average, first described in his 1995 book Smarter Trading, is a great example of how an ​AMA can self-adjust to adapt to changing environments. Scott Cong draws inspiration from ​Kaufman's approach and proposes a new way to calculate the ​AMA smoothing factor.

█ CALCULATIONS

Following Perry Kaufman's approach, Scott Cong's ​AMA is calculated progressively as:
AMA = α * Close + (1 − α) * AMA(1),
where:

• Close = Close of the current bar
  
• AMA(1) = ​AMA value of the previous bar
  
• α = Smoothing factor between 0 and 1, defined by the lookback period
  

The smoothing factor determines the performance of ​AMA. In Cong's approach, it is calculated as:
α = Result / Effort,
where:

• Result = Highest price of the n period − Lowest price of the n period
  
• Effort = Sum(​TR, n), where ​TR stands for Wilder’s true range values of individual bars of the n period
  
• n = Lookback period
  

As the price range is always no greater than the total journey, α is ensured to be between 0 and 1.