OPEN-SOURCE SCRIPT
IIR Least-Squares Estimate
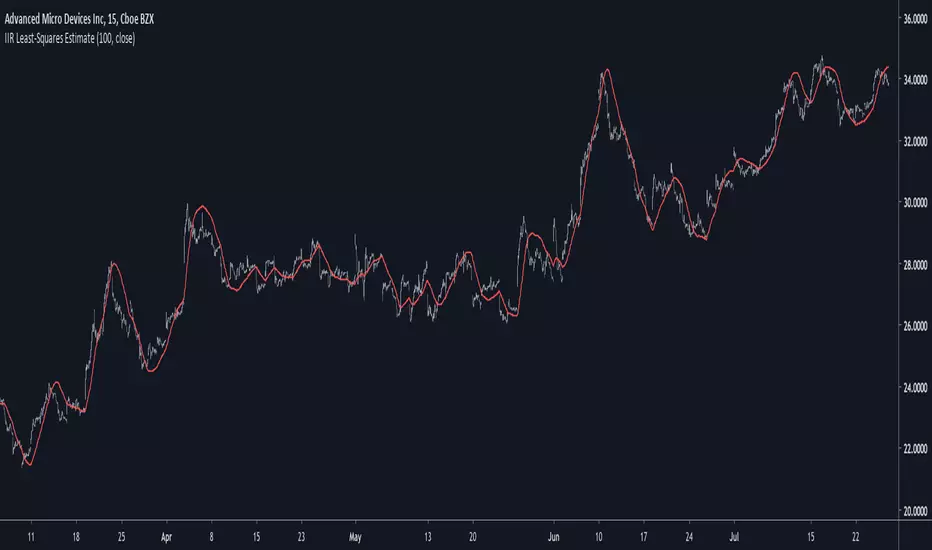
Introduction
Another lsma estimate, i don't think you are surprised, the lsma is my favorite low-lag filter and i derived it so many times that our relationship became quite intimate. So i already talked about the classical method, the line-rescaling method and many others, but we did not made to many IIR estimate, the only one was made using a general filter estimator and was pretty inaccurate, this is why i wanted to retry the challenge.
Before talking about the formula lets breakdown again what IIR mean, IIR = infinite impulse response, the impulse response of an IIR filter goes on forever, this is why its infinite, such filters use recursion, this mean they use output's as input's, they are extremely efficient.
The Calculation
The calculation is made with only 1 pole, this mean we only use 1 output value with the same index as input, more poles often means a transition band closer to the cutoff frequency.
Our filter is in the form of :
y = a*x+y - a*ema(y,length/2)
where y = x when t = 1 and y(1) when t > 2 and a = 4/(length+2)
This is also an alternate form of exponential moving average but smoothing the last output terms with another exponential moving average reduce the lag.
Comparison
Lets see the accuracy of our estimate.

Sometimes our estimate follow better the trend, there isn't a clear result about the overshoot/undershoot response, sometimes the estimate have less overshoot/undershoot and sometime its the one with the highest.


The estimate behave nicely with short length periods.
Conclusion
Some surprises, the estimate can at least act as a good low-lag filter, sometimes it also behave better than the lsma by smoothing more. IIR estimate are harder to make but this one look really correct.
If you are looking for something or just want to say thanks try to pm me :)
Thank for reading !
Another lsma estimate, i don't think you are surprised, the lsma is my favorite low-lag filter and i derived it so many times that our relationship became quite intimate. So i already talked about the classical method, the line-rescaling method and many others, but we did not made to many IIR estimate, the only one was made using a general filter estimator and was pretty inaccurate, this is why i wanted to retry the challenge.
Before talking about the formula lets breakdown again what IIR mean, IIR = infinite impulse response, the impulse response of an IIR filter goes on forever, this is why its infinite, such filters use recursion, this mean they use output's as input's, they are extremely efficient.
The Calculation
The calculation is made with only 1 pole, this mean we only use 1 output value with the same index as input, more poles often means a transition band closer to the cutoff frequency.
Our filter is in the form of :
y = a*x+y - a*ema(y,length/2)
where y = x when t = 1 and y(1) when t > 2 and a = 4/(length+2)
This is also an alternate form of exponential moving average but smoothing the last output terms with another exponential moving average reduce the lag.
Comparison
Lets see the accuracy of our estimate.
Sometimes our estimate follow better the trend, there isn't a clear result about the overshoot/undershoot response, sometimes the estimate have less overshoot/undershoot and sometime its the one with the highest.
The estimate behave nicely with short length periods.
Conclusion
Some surprises, the estimate can at least act as a good low-lag filter, sometimes it also behave better than the lsma by smoothing more. IIR estimate are harder to make but this one look really correct.
If you are looking for something or just want to say thanks try to pm me :)
Thank for reading !
Mã nguồn mở
Theo đúng tinh thần TradingView, tác giả của tập lệnh này đã công bố nó dưới dạng mã nguồn mở, để các nhà giao dịch có thể xem xét và xác minh chức năng. Chúc mừng tác giả! Mặc dù bạn có thể sử dụng miễn phí, hãy nhớ rằng việc công bố lại mã phải tuân theo Nội quy.
Check out the indicators we are making at luxalgo: tradingview.com/u/LuxAlgo/
"My heart is so loud that I can't hear the fireworks"
"My heart is so loud that I can't hear the fireworks"
Thông báo miễn trừ trách nhiệm
Thông tin và các ấn phẩm này không nhằm mục đích, và không cấu thành, lời khuyên hoặc khuyến nghị về tài chính, đầu tư, giao dịch hay các loại khác do TradingView cung cấp hoặc xác nhận. Đọc thêm tại Điều khoản Sử dụng.
Mã nguồn mở
Theo đúng tinh thần TradingView, tác giả của tập lệnh này đã công bố nó dưới dạng mã nguồn mở, để các nhà giao dịch có thể xem xét và xác minh chức năng. Chúc mừng tác giả! Mặc dù bạn có thể sử dụng miễn phí, hãy nhớ rằng việc công bố lại mã phải tuân theo Nội quy.
Check out the indicators we are making at luxalgo: tradingview.com/u/LuxAlgo/
"My heart is so loud that I can't hear the fireworks"
"My heart is so loud that I can't hear the fireworks"
Thông báo miễn trừ trách nhiệm
Thông tin và các ấn phẩm này không nhằm mục đích, và không cấu thành, lời khuyên hoặc khuyến nghị về tài chính, đầu tư, giao dịch hay các loại khác do TradingView cung cấp hoặc xác nhận. Đọc thêm tại Điều khoản Sử dụng.