Polynomial LSMA Estimation - Estimating An LSMA Of Any Degree

4 thg 9, 2019

Introduction

It was one of my most requested post, so here you have it, today i present a way to estimate an LSMA of any degree by using a kernel based on a sine wave series, note that this is originally a paper that i posted that you can find here figshare.com/articles/A_NEW_LOW-PASS_FIR_FILTER_FOR_SIGNAL_PROCESSING/9762863 , in the paper you will be able to find the frequency response of the filter as well as both python and pinescript code.

The least squares moving average or LSMA is a filter that best fit a polynomial function through the price by using the method of least squares, by default the LSMA best fit a line through the input by using the following formula : ax + b where x is often a linear series 1,2,3...etc and a/b are parameters, the LSMA is made by finding a and b such that their values minimize the sum of squares between the lsma and the input.

Now a LSMA of 2nd degree (quadratic) is in the form of ax^2 + bx + c, although the first order LSMA is not hard to make the 2nd order one is way more heavy in term of codes since we must find optimal values for a,b and c, therefore we may want to find alternatives if the goal is simply data smoothing.

Estimation By Convolution

The LSMA is a FIR filter which posses various characteristics, the impulse response of an LSMA of degree n is a polynomial of the same degree, and its step response is a polynomial of degree n+1, estimating those step response is done by the described sine wave series :

f(x) =>
sum = 0.
b = 0.
pi = atan(1)*4
a = x*x
for i = 1 to d
b := 1/i * sin(x*i*pi)
sum := sum + b
pol = a + iff(d == 0,0,sum)

which is simple the sum of multiple sine waves of different frequency and amplitude + the square of a linear function. We then differentiate this result and apply convolution.

The Indicator

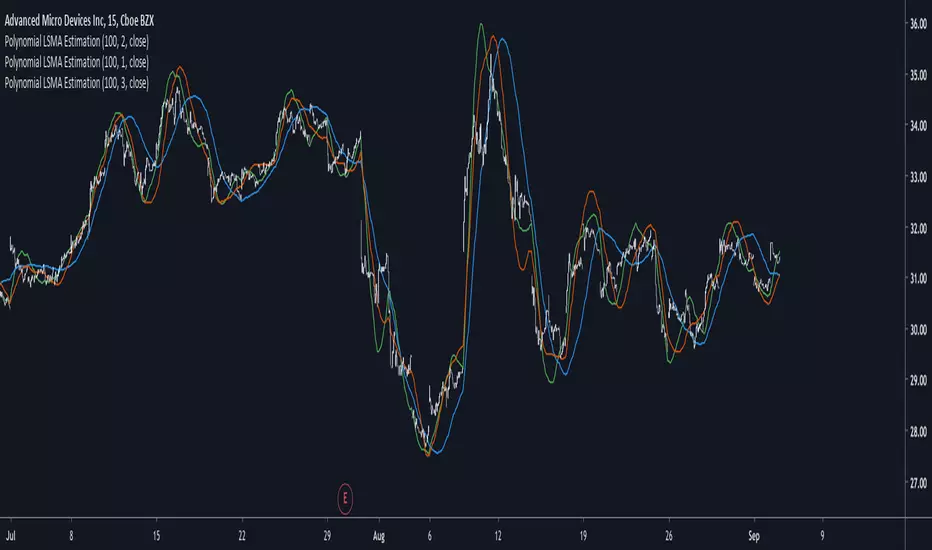
length control the filter period while degree control the degree of the filter, higher degree's create better fit with the input as seen below :



Now lets compare our estimate with actual LSMA's, below a lsma in blue and our estimate in orange of both degree 1 and period 100 :



Below a LSMA of degree 2 (quadratic) and our estimate with degree 2 with both period 100 :



It can be seen that the estimate is doing a pretty decent job.

Now we can't make comparisons with higher degrees of lsma's but thats not a real necessity.

Conclusion

This indicator wasn't intended as a direct estimate of the lsma but it was originally based on the estimation of polynomials using sine wave series, which led to the proposed filter showcased in the article. So i think we can agree that this is not a bad estimate although i could have showcased more statistics but thats to many work, but its not that interesting to use higher degree's anyways so sticking with degree 1, 2 and 3 might be for the best.

Hope you like and thanks for reading !